LORE...: Trigonomeria

jueves, 22 de abril de 2010

Trigonomeria

-Trigonometría: es una rama de la matemática,cuya significado etimológico es "la medición de los triángulos".
-La tangente es la relación del seno entre el coseno, según la definición ya expuesta

Identidades trigonométricas

-Una identidad es una igualdad en que se cumple para todos los valores permisibles de la variable. En trigonometría existen seis identidades fundamentales:

Recíprocas

$\operatorname {sen} (\alpha) \cdot \csc (\alpha) = 1$

$\operatorname {cos} (\alpha) \cdot \sec (\alpha) = 1$

$\operatorname {tan} (\alpha) \cdot \cot (\alpha) = 1$

De división

$\tan (\alpha) = \frac {\operatorname {sen} (\alpha)}{ \cos (\alpha)}$

Por el teorema de Pitágoras

Como en el triángulo rectángulo cumple la funcion que:

$a^2 + b^2 = c^2 \,$

de la figura anterior se tiene que:

$\operatorname {sen} (\alpha ) = \frac {a}{c}$

$cos (\alpha ) = \frac {b}{c}$

$c = 1 \,$

entonces para todo ángulo α, se cumple la identidad Pitagórica :

$\operatorname {sen}^2 \alpha + \cos^2 \alpha = 1 \,$

que también puede expresarse:

$\tan^2 \alpha + 1 = \sec^2 \alpha \,$

$1+\cot^2 \alpha = \csc^2 \alpha \,$

El seno de un ángulo: es la razón entre el largo del cateto opuesto del ángulo dividido por el largo de la hipotenusa.

El coseno de un ángulo:

es la razón entre el largo del cateto adyacente al ángulo dividido por el largo de la hipotenusa.

La tangente de un ángulo: es la razón entre el largo del cateto opuesto del ángulo dividido por el largo del lado adyacente del ángulo.

La Cotangente, abreviado como cot o cta, es la razón Trigonométrica recíproca de la Tangente, o también su inverso multiplicativo:

$\cot \alpha = \frac{1}{\tan \alpha} = \frac{b}{a}$

-La Secante, (abreviado como sec), es la razón Trigonométrica recíproca del coseno, o también su inverso multiplicativo:

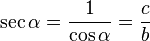
$\sec \alpha = \frac{1}{\cos \alpha} = \frac{c}{b}$

La Cosecante (abreviado como csc o cosec) es la razón trigonométrica recíproca del seno, o también su inverso multiplicativo:

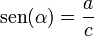
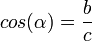
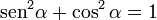
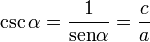
$\csc \alpha = \frac{1}{\operatorname {sen} \alpha} = \frac{c}{a}$

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)